Alg.15.数据结构-堆

二叉堆

• 结构性：二叉堆是一个完全填满的二叉树（叶子节点都集中在左边）；
• 堆序性：父节点的键值总是大于或等于（小于或等于）任何一个子节点的键值：如果父节点的键值总是小于或等于子节点（根节点的值是最小的）, 那么称为小顶堆（min heap），反正择称为大顶堆（max heap）

二叉堆一般用数组来表示。如果根节点在数组中的位置是1，第_n_个位置的子节点分别在2_n_和 2_n_+1。因此，第1个位置的子节点在2和3，第2个位置的子节点在4和5。以此类推。这种基于1的数组存储方式便于寻找父节点和子节点。

如果存储数组的下标基于0，那么下标为 _i_ 的节点的子节点是 2i + 1 与 2i + 2 ；其父节点的下标是 floor((i − 1) ∕ 2)。函数 floor(x) 的功能是“向下取整”，或者说“向下舍入”，即取不大于 _x_ 的最大整数（与“四舍五入”不同，向下取整是直接取按照数轴上最接近要求值的左边值，即不大于要求值的最大的那个值）。比如 floor(1.1)、floor(1.9) 都返回1。

如下图的两个堆：

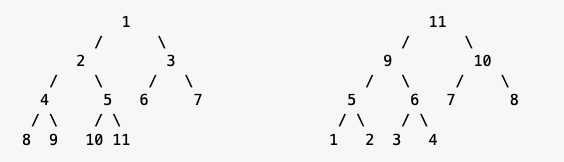
将这两个堆保存在以1开始的数组中：

位置:  1  2  3  4  5  6  7  8  9 10 11
左图:  1  2  3  4  5  6  7  8  9 10 11
右图: 11  9 10  5  6  7  8  1  2  3  4

对于一个很大的堆，使用连续数组这种存储是低效的。因为节点的子节点很可能在另外一个内存页中。B-heap是一种效率更高的存储方式，把每个子树放到同一内存页。

如果用指针链表存储堆，那么需要能访问叶节点的方法。可以对二叉树“穿线”(threading)方式，来依序遍历这些节点。

@ref: 二叉堆 - 维基百科，自由的百科全书

插入操作

在数组的最末尾插入新节点。然后自下而上调整子节点与父节点（称作 up-heap 或 bubble-up, percolate-up, sift-up, trickle up, heapify-up, cascade-up 操作）：比较当前节点与父节点，不满足”堆性质”则交换。从而使得当前子树满足二叉堆的性质。复杂度 = O(logn)

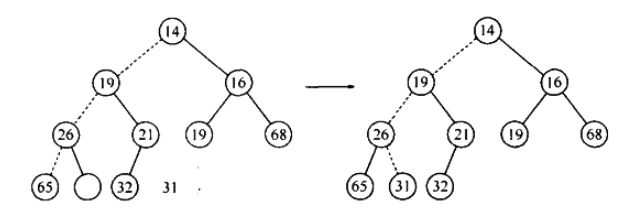
插入操作需要维持堆序性，下图是向堆插入 14 的过程：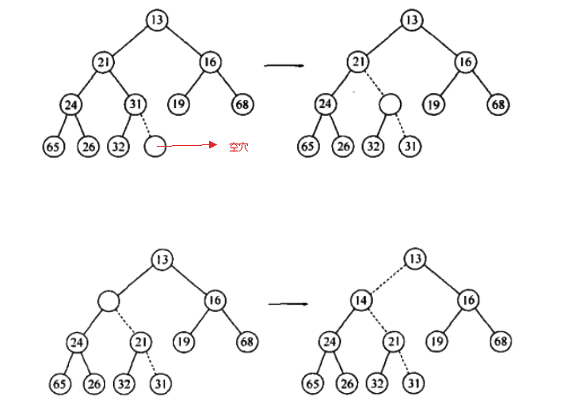

• 为将一个元素 X 插入到堆中，我们在下一个可用位置创建一个空穴，否则该堆将不是完全树。
• 如果 X 可以放在该空穴中而不破坏堆的序，那么插入完成。否则，我们把空穴的父节点上的元素移入该空穴中，这样，空穴就朝着根的方向上冒一步。继续改过程直到 X 能被放入空穴中为止。
• 这种实现过程称之为上滤：新元素在堆中上滤直到找出正确的插入位置。

删除操作

对于最大堆，删除根节点就是删除最大值；对于最小堆，是删除最小值。然后，把堆存储的最后那个节点移到填在根节点处。再从上而下调整父节点与它的子节点：对于最大堆，父节点如果小于具有最大值的子节点，则交换二者。这一操作称作down-heap或bubble-down, percolate-down, sift-down, trickle down, heapify-down, cascade-down,extract-min/max等。直至当前节点与它的子节点满足“堆性质”为止。

删除操作以小顶堆为例，找到的最小元素非常容易，但删除堆顶后还需要维持完全树，下图是删除堆顶 13 元素的过程：

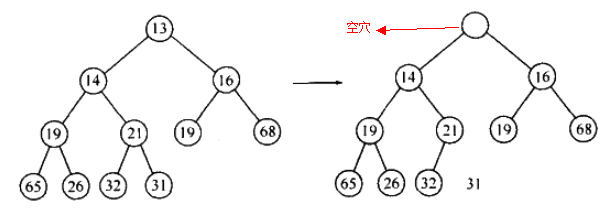
• 首先我们删除根元素13,建立一个空穴,之后判断元素31是否可以放入这个空穴中, 也即先判断最右叶子，如果能直接移动最好，无需再维护完全树
• 无法直接移动，所以空穴下滑（向左儿子方向），再判断 31 能否插入空穴，不能，继续下滑：

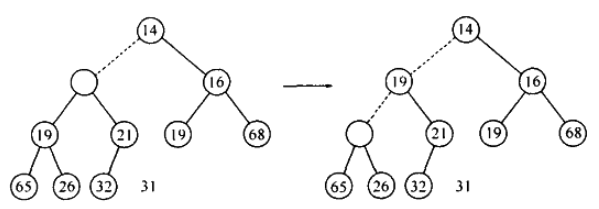
• 最后 26 置入空穴中，同时空穴下滑到叶子层，31 可以置入空穴，结束：

• 这一种操作过程称之为下滤:空穴一步步下滑.

PriorityQueue 源码分析

PriorityQueue 是 JDK 中自带的优先级队列，使用小顶堆实现，有如下方法：

• 入队：add、offer 方法，如果失败，add 抛异常，offer 返回 false
• 获取队头：element、peek 返回堆顶最小的元素，但不删除队头（堆顶）
• 出队：remove、poll 返回并删除队头（堆顶）最小的元素

offer()

offer()方法：插入元素到合适的位置

//offer(E e)
public boolean offer(E e) {
    if (e == null)//不允许放入null元素
        throw new NullPointerException();
    modCount++;
    int i = size;
    if (i >= queue.length)
        grow(i + 1);//自动扩容
    size = i + 1;
    if (i == 0)//队列原来为空，这是插入的第一个元素
        queue[0] = e;
    else
        siftUp(i, e);//调整
    return true;
}

上述代码中，扩容函数 grow() 类似于 ArrayList 里的 grow() 函数，就是再申请一个更大的数组，并将原数组的元素复制过去;

需要注意的是 siftUp(int k, E x) 方法，该方法用于插入元素 x 并维持堆的特性（上滤）。

//siftUp()
private void siftUp(int k, E x) {
    while (k > 0) {
        int parent = (k - 1) >>> 1;//parentNo = (nodeNo-1)/2
        Object e = queue[parent];
        if (comparator.compare(x, (E) e) >= 0)//调用比较器的比较方法
            break;
        queue[k] = e;
        k = parent;
    }
    queue[k] = x;
}

新加入的元素 x 可能会破坏小顶堆的性质，因此需要进行调整。调整的过程为：从 k 指定的位置开始，将 x 逐层与当前点的 parent 进行比较并交换，直到满足 x >= queue[parent] 为止。

poll()

poll 方法：删除堆顶，并维护堆序性

public E poll() {
    if (size == 0)
        return null;
    int s = --size;
    modCount++;
    E result = (E) queue[0];//0下标处的那个元素就是最小的那个
    E x = (E) queue[s];
    queue[s] = null;
    if (s != 0)
        siftDown(0, x);//调整
    return result;
}

上述代码首先记录 0 下标处的元素，并用最后一个元素替换 0 下标位置的元素，之后调用 siftDown() 方法对堆进行调整，最后返回原来 0 下标处的那个元素（也就是最小的那个元素）。重点是 siftDown(int k, E x) 方法，该方法的作用是从 k 指定的位置开始，将 x 逐层向下与当前点的左右孩子中较小的那个交换，直到 x 小于或等于左右孩子中的任何一个为止。

//siftDown()
private void siftDown(int k, E x) {
    int half = size >>> 1;
    while (k < half) {
        //首先找到左右孩子中较小的那个，记录到 c 里，并用 child 记录其下标
        int child = (k << 1) + 1;//leftNo = parentNo*2+1
        Object c = queue[child];
        int right = child + 1;
        if (right < size &&
            comparator.compare((E) c, (E) queue[right]) > 0)
            c = queue[child = right];
        if (comparator.compare(x, (E) c) <= 0)
            break;
        queue[k] = c;//然后用 c 取代原来的值
        k = child;
    }
    queue[k] = x;
}

@ref: https://www.cnblogs.com/Elliott-Su-Faith-change-our-life/p/7472265.html