图的概念
在图中的数据元素通常称为结点,V 是所有顶点的集合,E 是所有边的集合。如果两个顶点 v, w,只能由 v 向 w,而不能由 w 向 v,那么我们就把这种情况叫做一个从 v 到 w 的有向边。v 也被称做初始点,w 也被称为终点。这种图就被称做有向图。
如果v和w是没有顺序的,从v到达w和从w到达v是完全相同的,这种图就被称为无向图。
假如,图中的结点个数为 n,那么在一个无向图,假设每对结点之间只能有一条边,那么这个无向图中的边数最多只有 $ 1/2 n (n-1) $。边数最多的无向图也叫完全图。
同样的,对于有向图,边数最多有 $ n(n-1) $ 个,边数最多的有向图叫有向完全图。
如果图中的边数很少,这种图也被叫稀疏图。稀疏图是一种大约的概念,并没有一定的数值,说边数低于这个数值的时候就是稀疏图,在不同的场景下,稀疏图的定义会不一样。反之,如果边数比较多,就称为稠密图。
有时图的边具有与它相关的数,这种与图的边相关的数就叫做权。例如,从A地到B地的车票是80块钱,那这个80就是这条路上的耗费,我们如果把这样的交通网做成一个图,就变成了一个带权有向图。这种图也被称为网络。
一个顶点如果有多个边与其相联,那么这些相联的边数就称为点的度。如果是有向图,那么初始点就有出度,而终点则有入度。
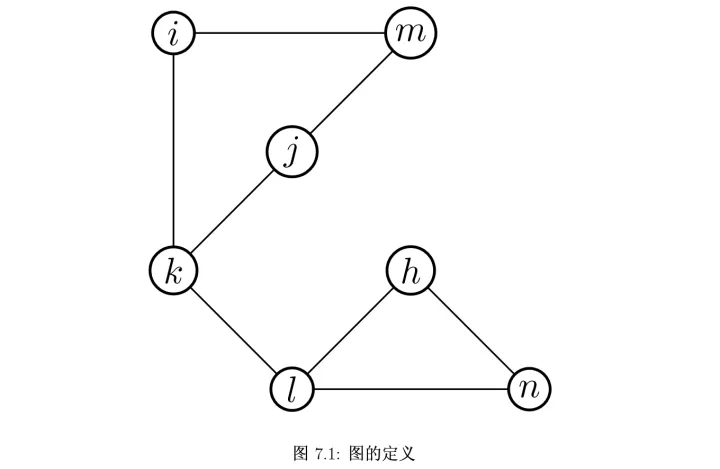
图的表达
邻接矩阵
使用二维数组来表示一个图:
对于图 G,假如其中有 n 个结点,我们可以定义一个二维数组 A[n][n],如果顶点 Vi 和顶点 Vj 之间存在边 Eij,那么就将 A[i][j] 设为1,否则设为0。就称二维数组 A 是图 G 的邻接矩阵。
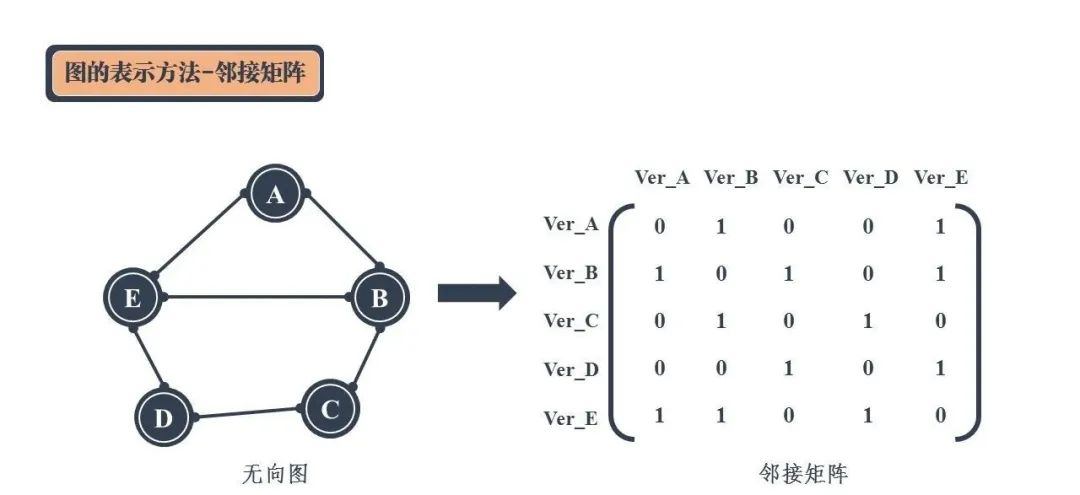
如果图 G 是无向图,那么,如果 A[i][j] 为1,可以推知 A[j][i] 也为1(对称)。如果 G 是有向图(见下图),则不存在这个规律。
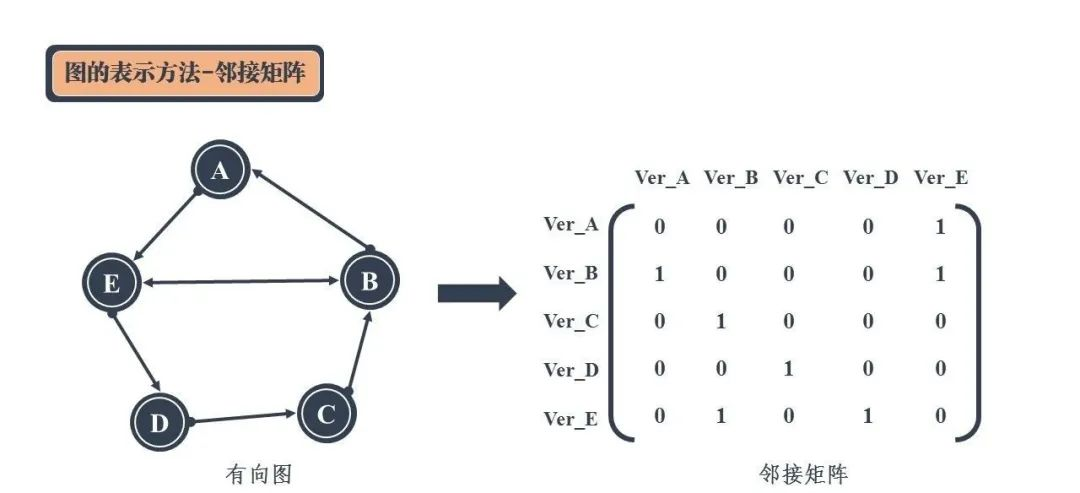
如果 G 的边上有权重,图 G 是一个带权有向图,顶点顶点 Vi 和顶点 Vj 之间存在边 Eij,且 Eij 的权重为 Wij,就令 A[i][j] 的值为 Wij。如果两个顶点 Vi 和顶点 Vj 之间不存在边,那么就记 A[k][l]为无穷大。在实际的实现中可以使用整型的最大值代替。
➤ 复杂度分析:
在邻接矩阵中查询两个顶点是否相连的复杂度是O(1)_.
空间复杂度如何呢? 将图保存为邻接矩阵的空间复杂度是 O(n^2),其中 n 是顶点的数目。也可表示为 O(|V|2)。
添加一个顶点的运行时间如何呢?顶点被保存在 VxV 矩阵中。因此,每次添加顶点时,矩阵必须被重构为新的(V+1)x(V+1),在邻接矩阵中添加顶点的复杂度是 O(|V|^2)
邻接表
显然,用邻接矩阵并不适合表达一个稀疏图,不仅有空间上的浪费,另外二维数组的时间 & 空间复杂度都是 N^2
另外一种比较直接的思路就是使用多向链表。
用一个结构体表示图的一个节点,结构体中包含数据域和多个指针,其中数据域存储该顶点的信息,指针指向有连接的其他节点。
这样做的一个缺点是,由于图中各个节点的度数各不相同,最大度数和最小度数可能相差很多,因此,若按度数最大的顶点设计结点结构,则会浪费很多存储单元。而如果按照每个顶点自己的度数设计不同的结点结构,所带来的编程的复杂度得不偿失。
所以,我们就用一种改进的方案:使用链表代表一个结点,这种方案被称为邻接表。
在邻接表中,图中的每一个节点都用一个链表表示。设链表 i 对应节点 i,链表 i 中每个元素都表示节点 i 的一条边。
链表中的每个结点都由 3 个域组成:链表中的每个结点都由3个域组成,其中邻接点域表示与vi 相邻的点,例如与vi相 邻的vj,这个结点就是vj;链(nextArc)代表顶点i与顶点j之间的边eij;数据域(info)存储和边 相关的信息,例如权重等。
例如下面一个图: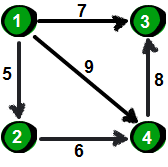
用邻接表表示则为: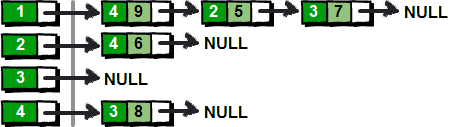
➤ 复杂度分析:
给定邻接表中两个节点是否相连的复杂度是 O(n), 其中 n 代表顶点的数量. 也可以写为 O(|V|). 你可以想象, 如果你想知道一个节点与另一个节点是否相连, 你必须遍历这个列表.
那么空间复杂度又如何呢? 将图存储为邻接表的空间复杂度是 O(n), 其中 n 是顶点数与边数的和. 也可以表示为 O(|V| + |E|).
上面这种实现方法为图中的每一个顶点(左边部分)都建立了一个单链表(右边部分)。这样我们就可以通过遍历每个顶点的链表,从而得到该顶点所有的边了。
通过邻接表可以获得从某个顶点出发能够到达的顶点,从而省去了对不相连顶点的存储空间。然而上面的邻接表只能表示顶点的“出度”,但没有表示“入度”。
这个问题很好解决,那就是增加一个表用来存储能够到达某个顶点的相邻顶点。这个表称作逆邻接表。
➤ 逆邻接表
逆邻接表与邻接表结构类似,只不过图的顶点链接着能够到达该顶点的相邻顶点。也就是说,邻接表时顺着图中的箭头寻找相邻顶点,而逆邻接表时逆着图中的箭头寻找相邻顶点。
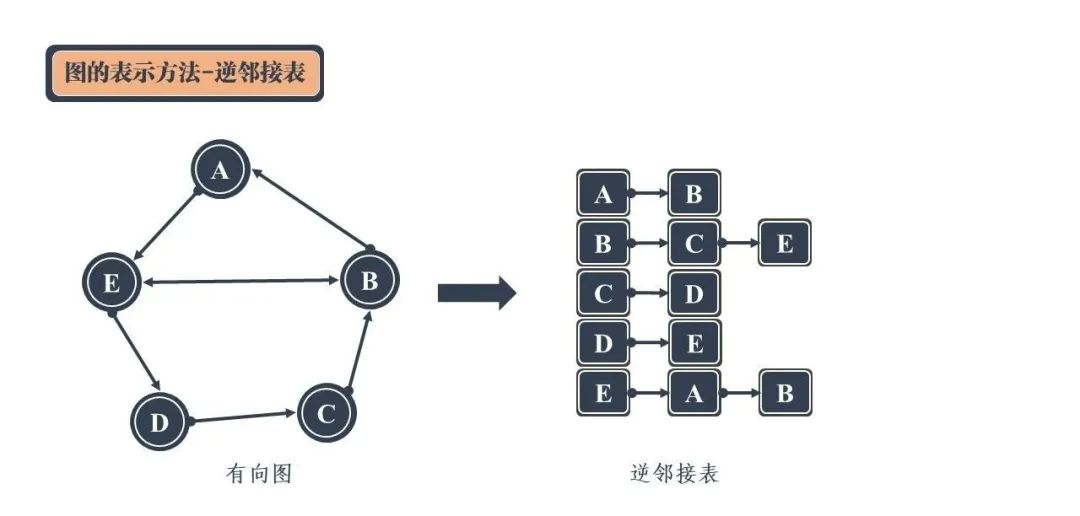
邻接表和逆邻接表的共同使用下,就能够把一个完整的有向图结构进行表示。可以发现,邻接表和逆邻接表实际上有一部分数据时重合的,因此可以将两个表合二为一,从而得到了所谓的十字链表:
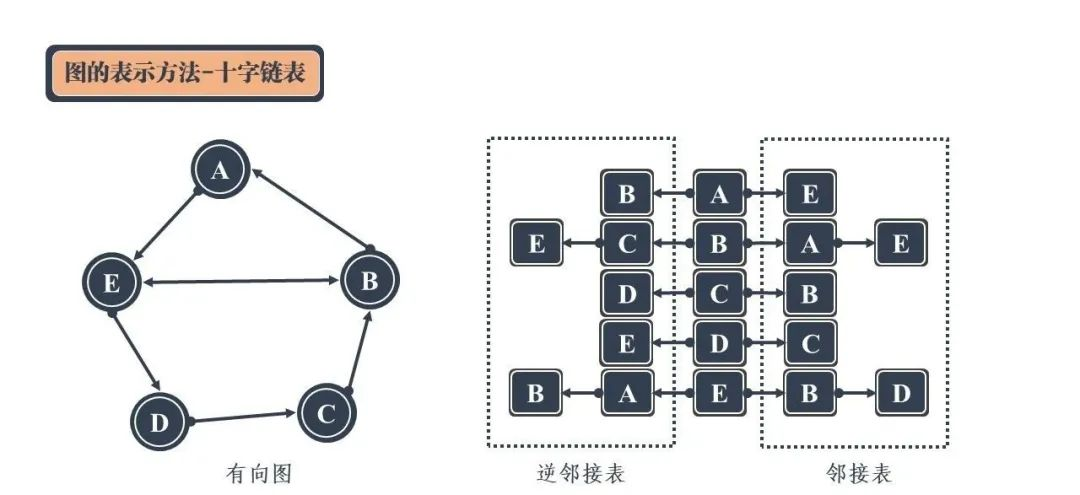
但这并不是最优的表示方式。虽然这样的方式共用了中间的顶点存储空间,但是邻接表和逆邻接表的链表节点中重复出现的顶点并没有得到重复利用,反而是进行了再次存储。因此,上图的表示方式还可以进行进一步优化。
十字链表优化后,可通过扩展的顶点结构和边结构来进行正逆邻接表的存储:(下面的弧头可看作是边的箭头那端,弧尾可看作是边的圆点那端)
data:用于存储该顶点中的数据; firstin指针:用于连接以当前顶点为弧头的其他顶点构成的链表,即从别的顶点指进来的顶点; firstout指针:用于连接以当前顶点为弧尾的其他顶点构成的链表,即从该顶点指出去的顶点;
边结构通过存储两个顶点来确定一条边,同时通过分别代表这两个顶点的指针来与相邻顶点进行链接:
tailvex:用于存储作为弧尾的顶点的编号; headvex:用于存储作为弧头的顶点的编号; headlink 指针:用于链接下一个存储作为弧头的顶点的节点; taillink 指针:用于链接下一个存储作为弧尾的顶点的节点;
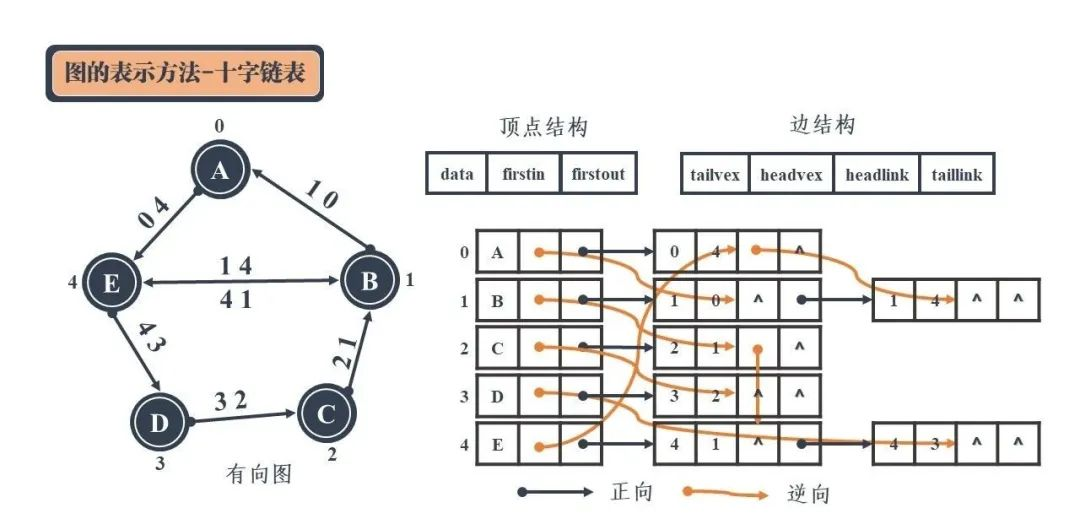
以上图为例子,对于顶点 A 而言,其作为起点能够到达顶点 E。因此在邻接表中顶点 A 要通过边 AE(即边04)指向顶点 E,顶点 A 的 firstout 指针需要指向边04的 tailvex。同时,从 B 出发能够到达 A,所以在逆邻接表中顶点 A 要通过边 AB(即边10)指向 B,顶点 A 的 firstin 指针需要指向边10的弧头,即 headlink 指针。依次类推。
十字链表采用了一种看起来比较繁乱的方式对边的方向性进行了表示,能够在尽可能降低存储空间的情况下增加指针保留顶点之间的方向性。具体的操作可能一时间不好弄懂,建议多看几次上图,弄清指针指向的意义,明白正向和逆向邻接表的表示。
@ref:
深度优先和广度优先
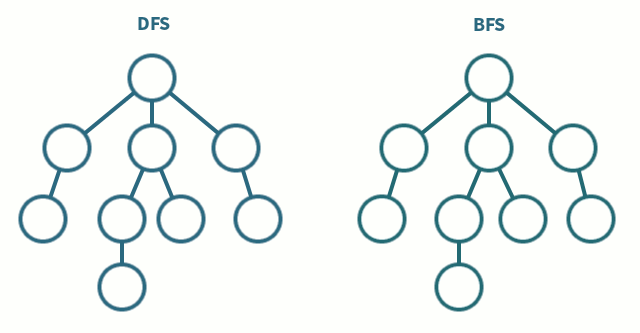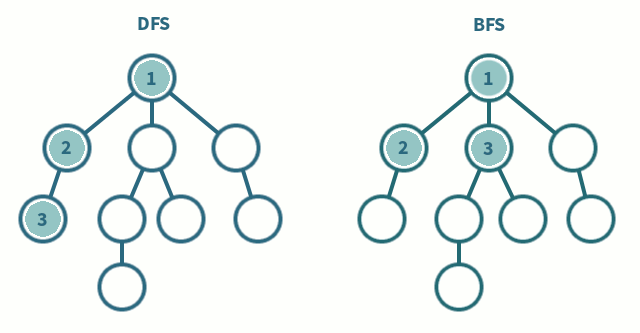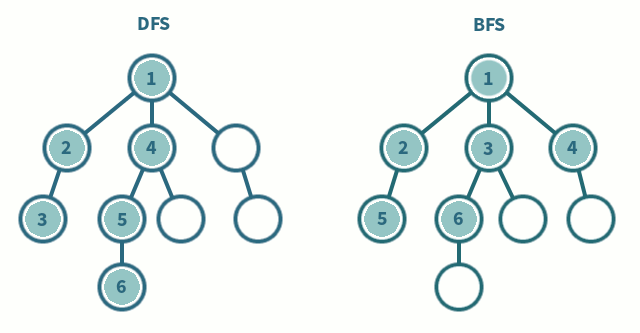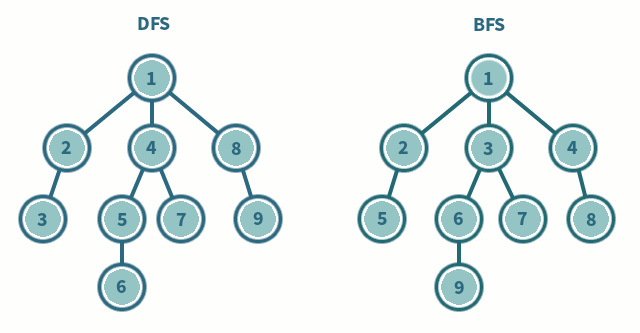
深度优先搜索
- 深度优先算法是一种优先遍历子节点而不是回溯的算法。
- 时间复杂度:
O(|V| + |E|)
广度优先搜索
- 广度优先搜索是优先遍历邻居节点而不是子节点的图遍历算法。
- 时间复杂度:
O(|V| + |E|)
拓扑排序
- 拓扑排序是对于有向图节点的线性排序,如果存在某条从 u 到 v 的边,则认为 u 的下标先于 v。
- 时间复杂度:
O(|V| + |E|)
Dijkstra 算法
- Dijkstra 算法 用于计算有向图中单源最短路径问题。
- 时间复杂度:
O(|V|^2)
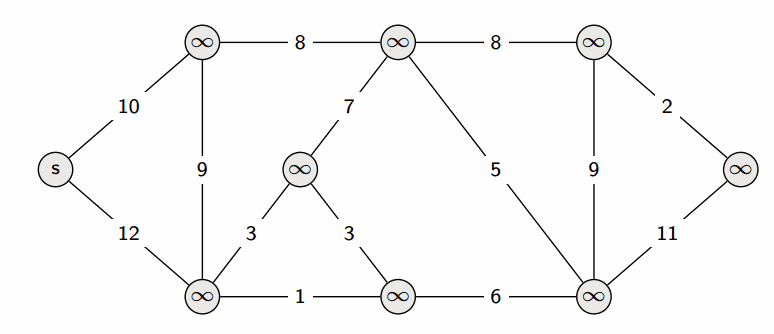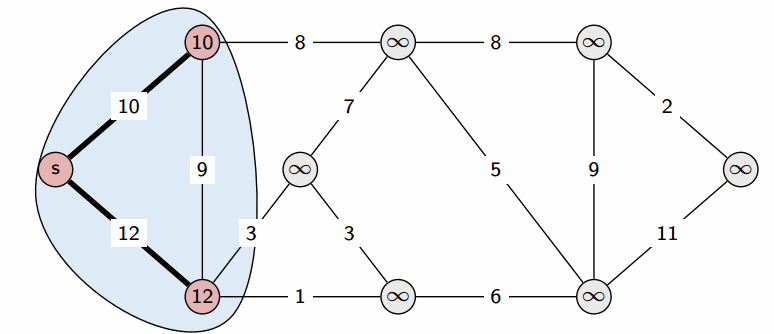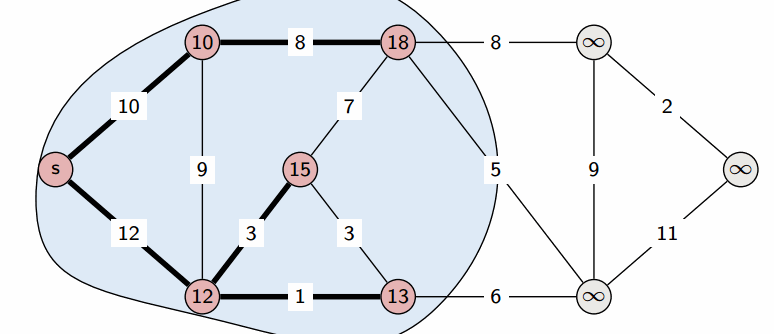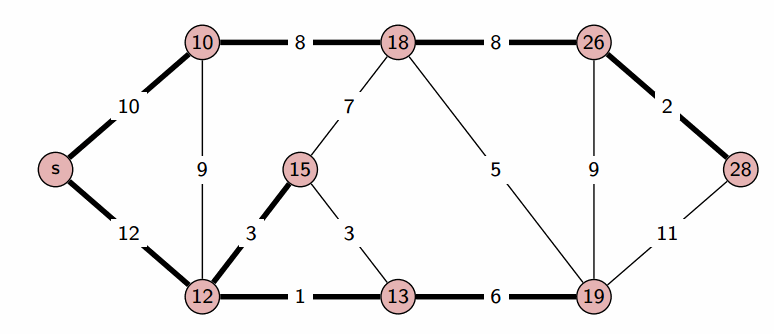
Bellman-Ford 算法
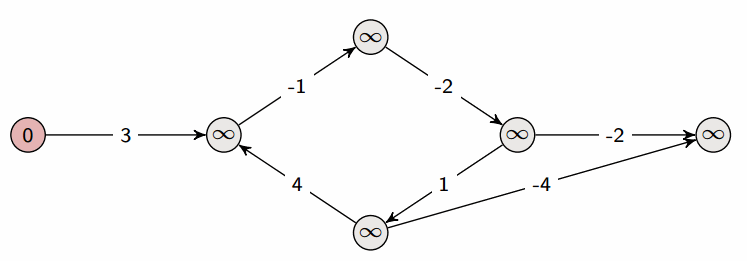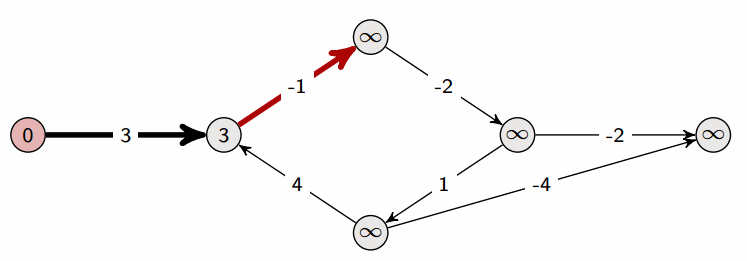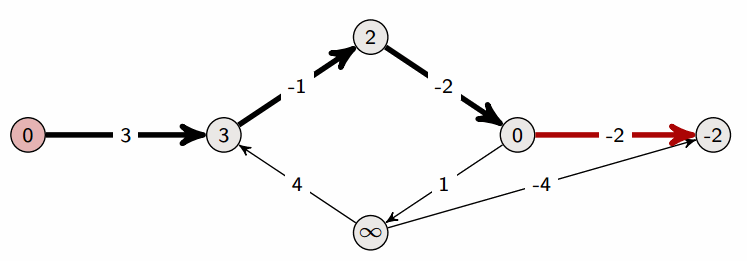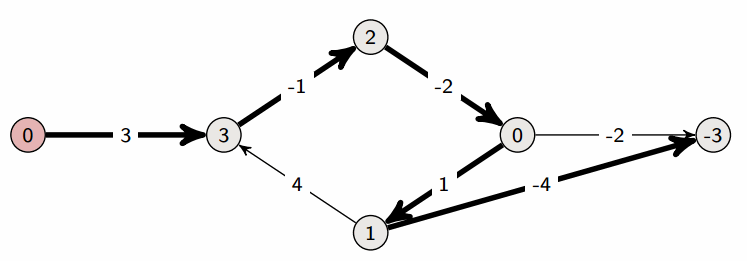
- Bellman-Ford 算法是在带权图中计算从单一源点出发到其他节点的最短路径的算法。
- 尽管算法复杂度大于 Dijkstra 算法,但是它适用于包含了负值边的图。
- 时间复杂度:
- 最优时间:
O(|E|) - 最坏时间:
O(|V||E|)
- 最优时间:
Floyd-Warshall 算法
- Floyd-Warshall 算法 能够用于在无环带权图中寻找任意节点的最短路径。
- 时间复杂度:
- 最优时间:
O(|V|^3) - 最坏时间:
O(|V|^3) - 平均时间:
O(|V|^3)
- 最优时间:
Prim 算法
- Prim 算法是用于在带权无向图中计算最小生成树的贪婪算法。换言之,Prim 算法能够在图中抽取出连接所有节点的边的最小代价子集。
- 时间复杂度:
O(|V|^2)
Kruskal 算法
- Kruskal 算法同样是计算图的最小生成树的算法,与 Prim 的区别在于并不需要图是连通的。
- 时间复杂度:
O(|E|log|V|)

参考
[[../_attachments/图数据结构入门 - 技术翻译 - OSCHINA 社区.pdf]]