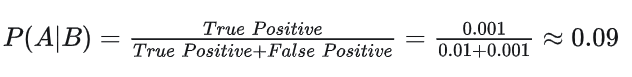@ref:: [[../_attachments/我所理解的贝叶斯定理 - 知乎.pdf|我所理解的贝叶斯定理 - 知乎]]
条件概率公式: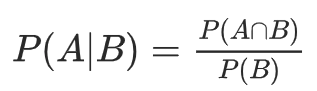
P(A∩B) 表示 A,B 事件同时发生的概率, P(A|B) 表示事件 A 在另一个事件 B 已经发生条件下的概率,即条件概率
全概率公式:移除了 P(A∩B) 等不容易观察的概率,表示P(A) 与P(A|B)..等等之间的关系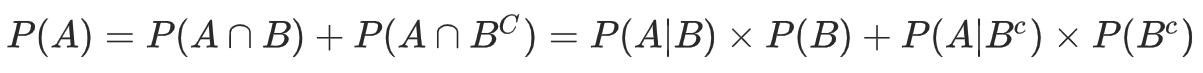
B^c 表示事件 B 的互补事件,从集合的角度来说是 B 的补集,
P(B) + P(B^c) = 1
条件概率和全概率可以用韦恩图表示:
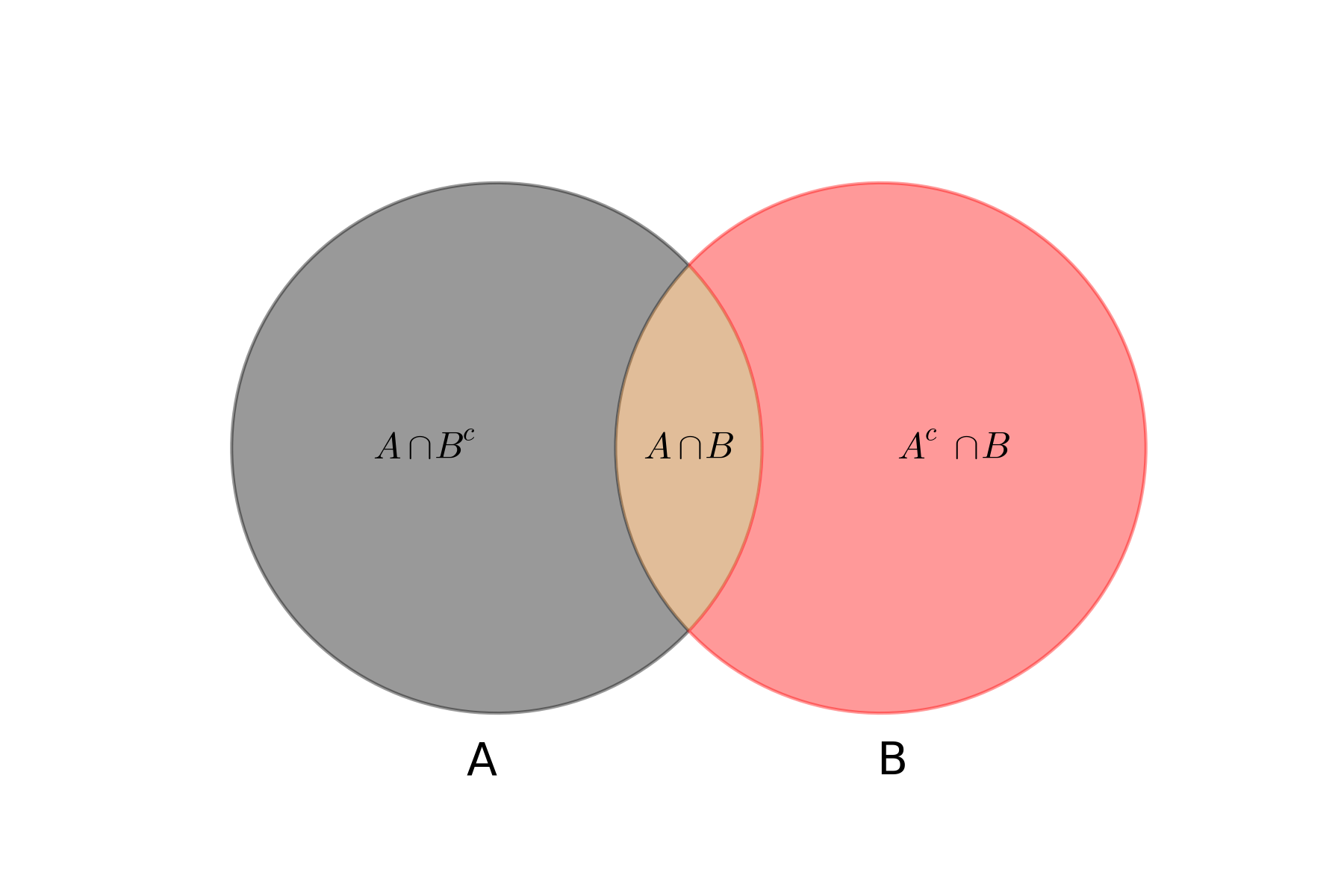
在条件概率和全概率的基础上,很容易推导出贝叶斯概率公式:
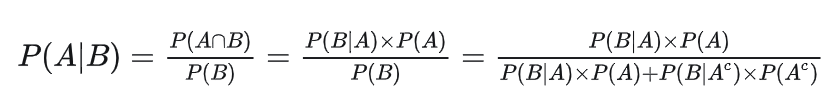
在贝叶斯定理中,每个名词都有约定俗成的名称:
- P(A|B) 是已知B发生后,A的条件概率,也成A的事后概率
- P(A) 是A的先验概率(或边缘概率),其不考虑任何B方面的因素
贝叶斯公式建立了 P(A|B) 同 P(B|A)、P(A)的边缘概率之间的关系,在实际问题中, P(B|A)、P(A)的概率更容易观测的情况下,贝叶斯公式方便计算实际概率问题
一个很有意思的例子:
假设某种疾病在所有人群中的感染率是0.1%,医院现有的技术对于该疾病检测准确率为 99%(已知患病情况下, 99% 的可能性可以检查出阳性;正常人 99% 的可能性检查为正常),如果从人群中随机抽一个人去检测,医院给出的检测结果为阳性,那么这个人实际得病的概率是多少?
很多人会脱口而出 “99%”,但真实概率远低于此,因为他们把两个后验概率搞混了,如果用 A 表示这个人患有该疾病,用 B 表示医院检测的结果是阳性,那么 P(B|A) = 99%, 表示的是「已知一个人得病的情况下医院检测出阳性的概率」;而我们现在问的是「对于随机抽取的这个人,已知检测结果为阳性的情况下这个人患病的概率」,即 P(A|B)
在实际生活中,几乎所有人(包括统计学者)都会无意识地将两个事件的后验概率混淆,即: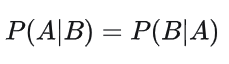
我们可以用贝叶斯定理来计算这个人实际得病的概率:
将上面的概率代入到贝叶斯公式中,可得: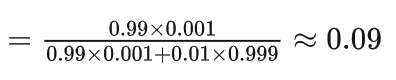
这个公式在这里的实际意义是什么?用混淆矩阵来解释(图中概率经过四舍五入,考虑到图片的尺寸,面积并没有和概率严格对应起来):

混淆矩阵的4种结果,分表表示 $$ A|B、A^c|B、A|B^c、A^c|B^c$$
在上面例子中,贝叶斯公式实际意义是: