约翰·拉里·凯利出生于1923年12月26日,二战期间凯利到了法定服役年龄,在海军航空部队当了4年飞行员,曾是二战期间的王牌飞行员。1953年他获得了物理学博士学位,博士论文题目为“不同材料的二阶弹性研究”,这项研究非常重要,使得凯利收到了贝尔实验室的工作邀请。这样30岁的凯利来到了贝尔实验室工作

该公式最早于1956年由物理学家约翰·L·凯利在《贝尔系统技术期刊》中发表,可以用来计算一个在期望净收益为正的独立重复赌局中,使本金长期增长率最大化的投注资金比例。

凯利公式和仓位管理
玩一个设定对你有利的游戏
假设现在有一个公平的投资游戏,获胜和失败的概率都是50%。如果获胜,玩家的收益率是40%;如果失败,玩家会亏损30%。
对于一个理性人来说,他一定会选择参加这个游戏,并且把这个游戏重复下去。
为什么呢?因为单次游戏的期望收益是正数,也就是说,游戏的设计对他是有利的。
举个例子,玩家投入1元钱,那么获胜可以取得1*(1+40%)=1.4元,而失败可以拿回1*(1-30%)=0.7元,这两种情况出现的概率都是50%,所以进行一次游戏后,玩家资产的期望是1.4*50%+0.7*50%=1.05元。玩家净赚0.05元,收益率5%。
在这样的情况下,如果初始资金是1元,游戏将重复100次,我们应该如何分配每次投资的仓位呢?
肯定会有朋友认为,既然单次游戏的结果这么有利,那岂不是投得越多,赚得越多?我每把都全仓梭哈不就好了吗?
——全仓梭哈会怎么样呢?
由于胜率是50%,出手100次,那么获胜的期望次数是50次,失败的次数也是50次,按此假定(当然实际情况可能会有差异)。则玩家最终的资产是:

说到这里,也许有的朋友还是不能理解,这看似优势满满的设定,是如何在全仓梭哈的过程中蚕食掉我们的资产的呢?
因为全仓梭哈的玩家,将自己过多的暴露在了“极端风险”当中,“十赌九输”也并不是一句玩笑话。
如果用凯利公式,可以计算出玩这个游戏单次投资的最佳仓位:
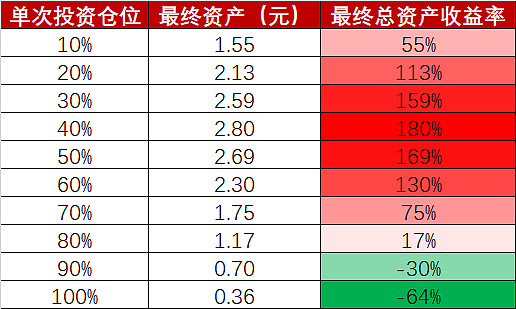
- 最佳的仓位设置是40%,使得资产直接增长1.8倍,而仓位高于或低于40%,起到的都是“副作用”;
- 每次只投资10%的仓位,最终也可实现55%的收益率;
- 全仓梭哈是最差的选择;
@ref: