@ref: 机器能像人一样思考吗?人工智能(一)机器学习和神经网络 - YouTube

人工智能发展史
- 1950:图灵测试提出(直到2014年才出现第一台通过图灵测试的程序)
- 1956:马文丶明斯基,约翰丶麦卡锡,香农 => 达特茅斯会议,第一次提出“AI”
- 1997:IBM深蓝战胜卡斯帕罗夫
- 辛顿(BP反向传播算法),杨立昆(CNN卷积神经网络),本吉奥获得2018年图灵奖
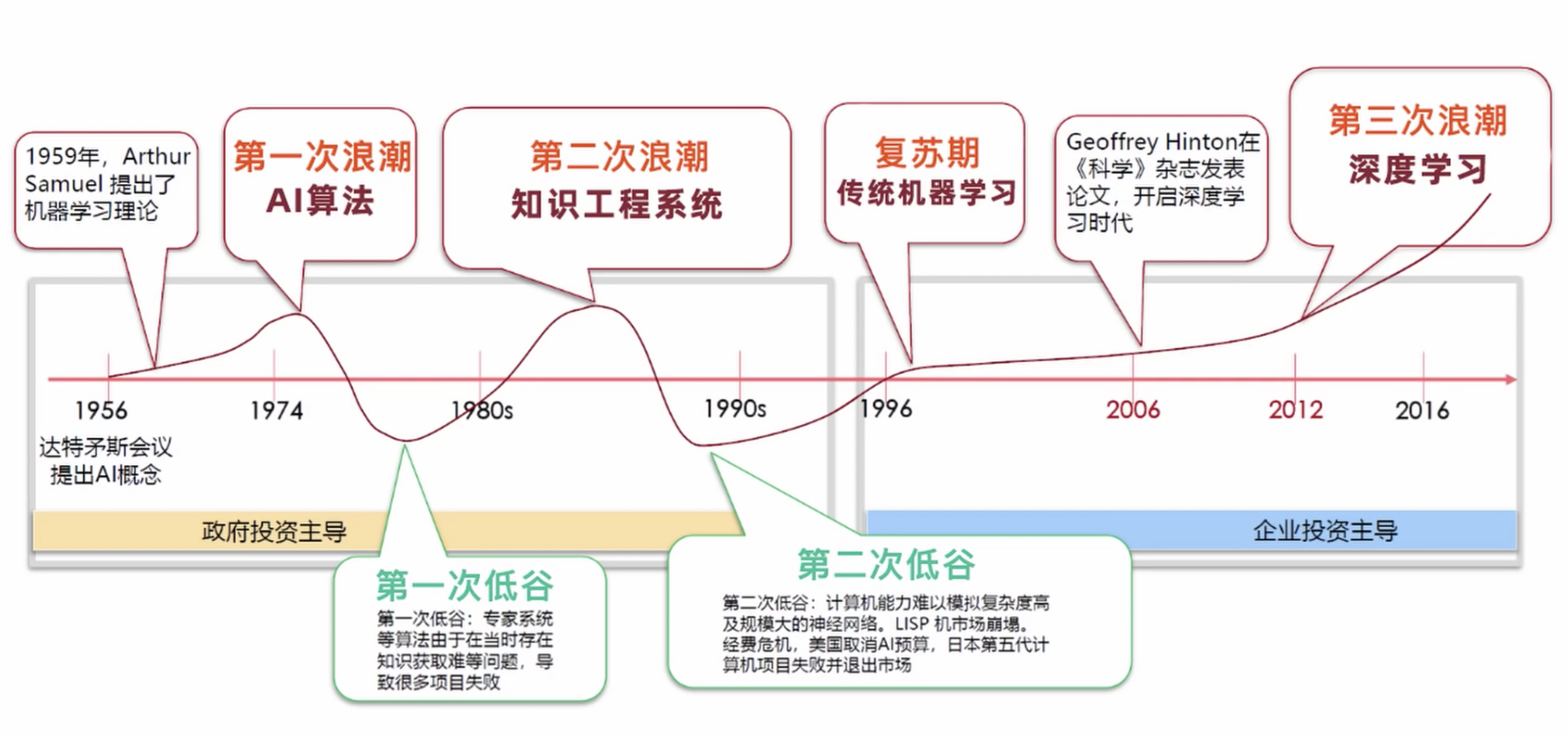
线性拟合 & 梯度下降算法
先看一个例子: 给出m组数据(x1,y1)~(xm,ym), 需要预测出y和x的函数关系.
线性拟合:「曲线拟合就是通过x,y的观测值来寻求参数b的最佳估计值,及寻求最佳的理论曲线y=f(x; b)。当函数y=f(x; b)为关于b的i线性函数时,称这种曲线拟合为线性拟合」
$$ y = wx +b $$
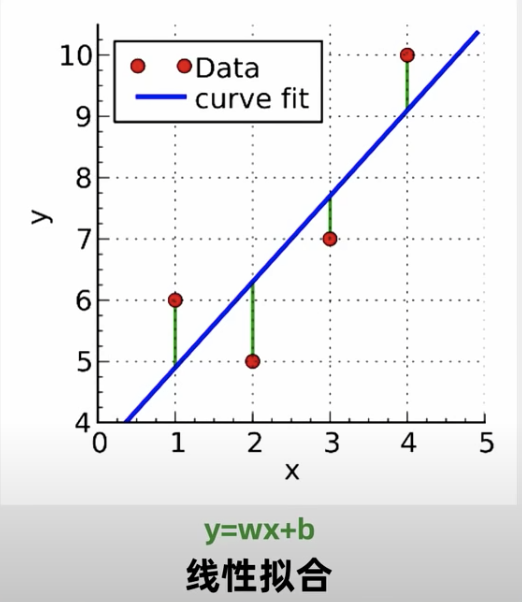
拟合曲线和实际的y的差值是Δy_i,由此给出损失函数J(m是样本个数):
$$ J = 1/2m ∑(Δy_i^2) = 1/2m ∑[y_i - (wx_i + b)]^2 $$
线性拟合的最优解, 即找到w(这里暂不考虑参数b)使J最小 ,
上例中只有2个参数,最小二乘可以解决,但是参数非常多就不适合了,这里需要梯度下降算法
求偏导数: $$ ∂y/∂w => w_{n+1} = w_n - η ∂y/∂w $$
通过多次迭代(从w0 →w1 →w2),找到到J最小时的w, 即梯度下降是算法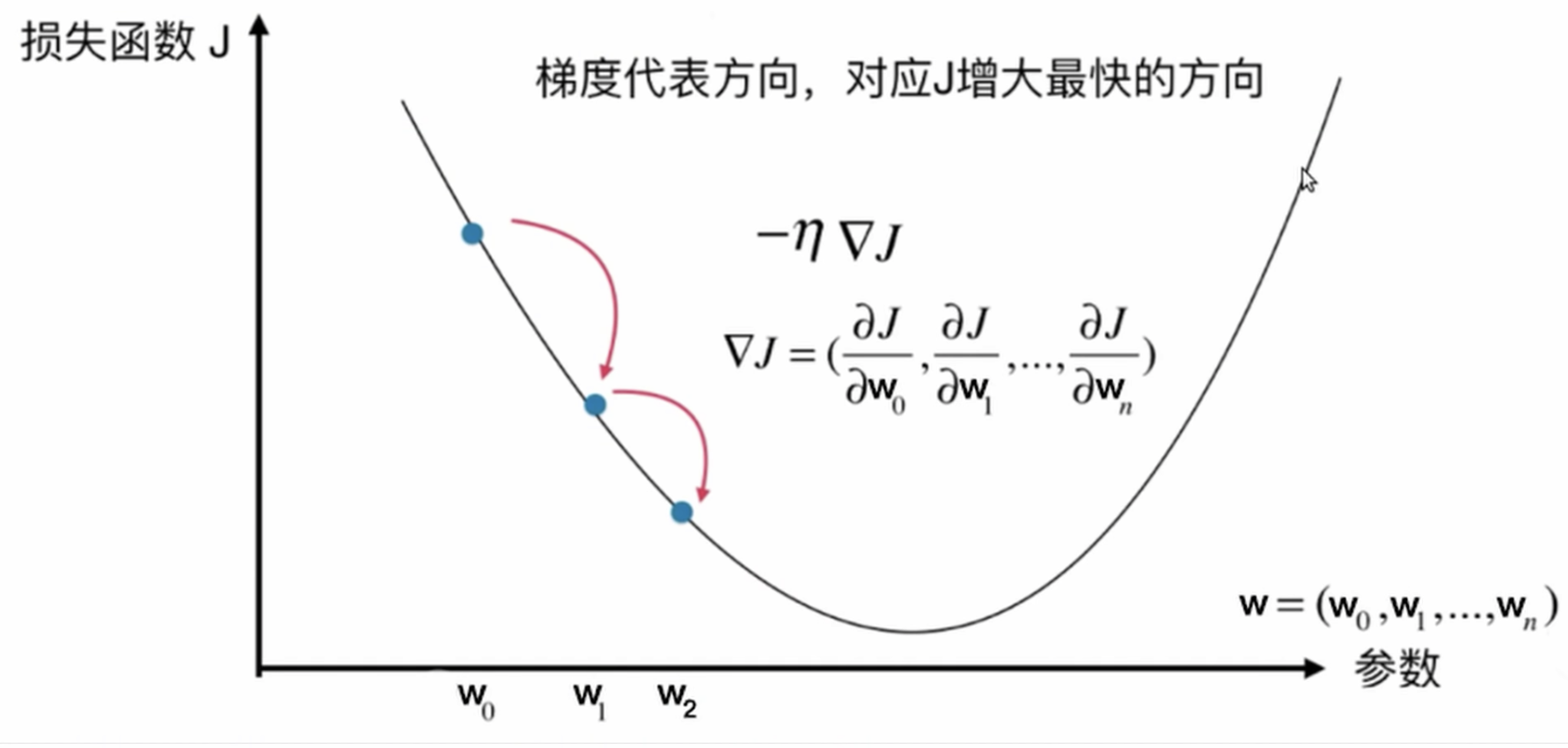
寻找参数最优值,使这也是模型训练的过程
神经网络(Neural Network)
典型神经元结构
M-P模型:每个神经元都有多个输入端(X1~Xn),W1j~Wnj是每个输入的参数,一个输出端Oj(但可以输出给多个刺激)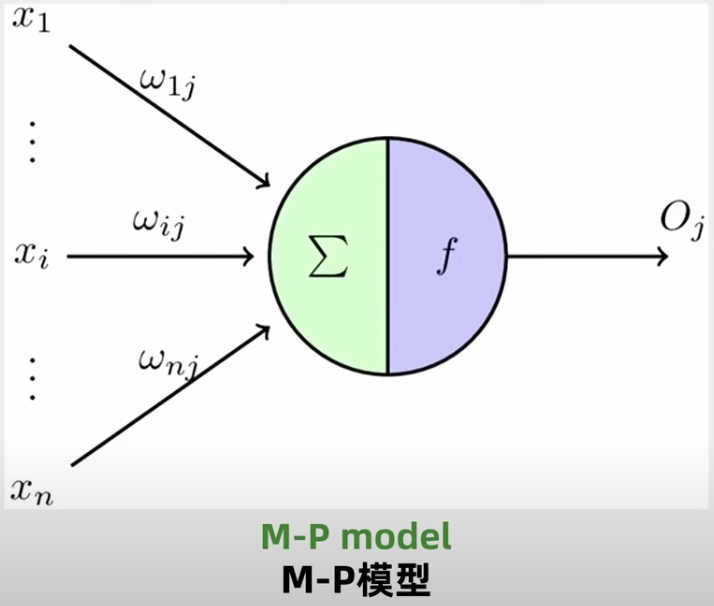
上图f即为激活函数(Sigmoid),决定是否向下一层输出,常用的如下: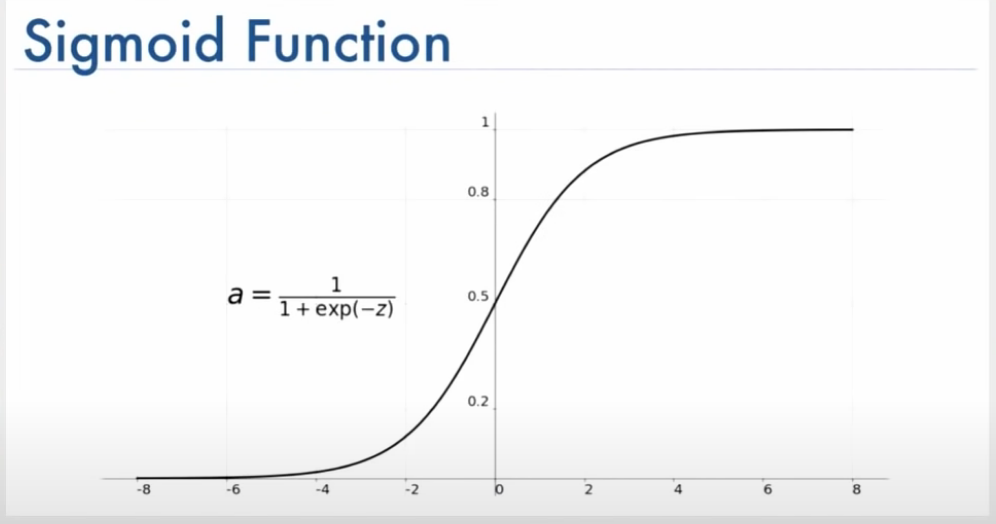
多个M-P模型的神经元组合为简单神经网络, 以及包含有更多隐层的多层神经网络(DNN):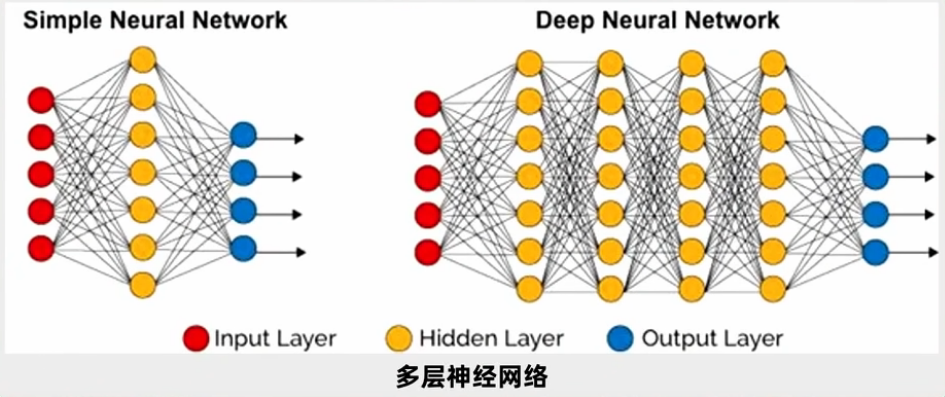
为了解决DNN调参复杂度(每层的链接对应的参数都需要调), 辛顿提出的反向传播(BP)算法:
从最后一层参数开始调, 然后调前一层的参数
卷积神经网络如何识别简单字母
卷积神经网络Convolutional Neural Networks
步骤1:卷积
• 卷积核:通常是3x3 or 5x5
• 原图像,对卷积核做卷积运算(每个位置相乘再相加,得到一个数)
• 最终得到“特征图”
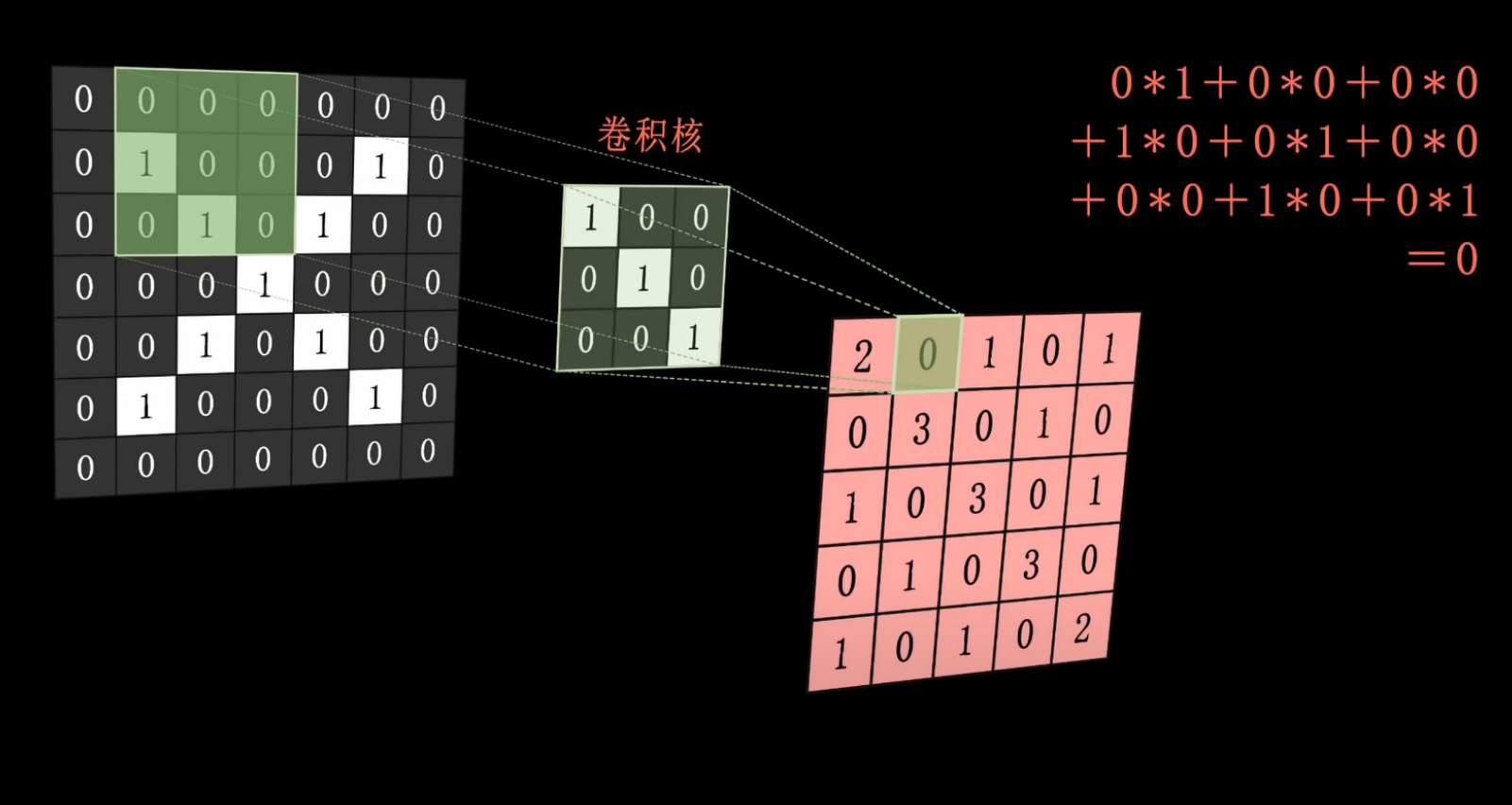
步骤2:池化、激活
这里用最大池化法,四个为一组(左上角2-0-0-3),选出最大的3,作为新的特征图的一个点:
对池化后的特征图,做激活处理: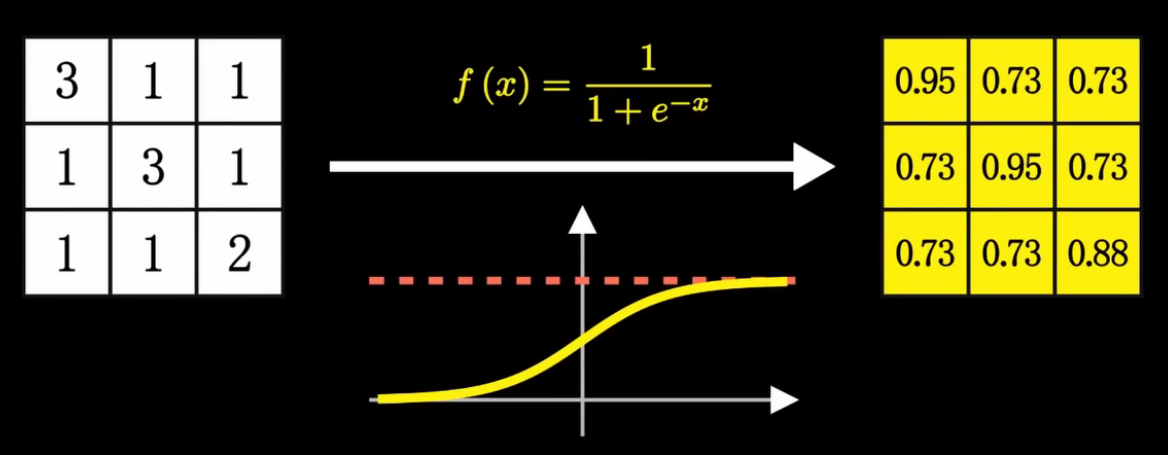

• 如果第一次卷积运算用了3个卷积核,那么会得到3个特征图(X-Y-Z)
• 3个特征图做池化处理,进一步减少数据量
• 3个特征图再次卷积运算(这次用了4个卷积核),那么得到4个特征图
下图是第二次卷积 (输入=3个特征图,4个卷积核,每个核都是3维,输出=4个特征图)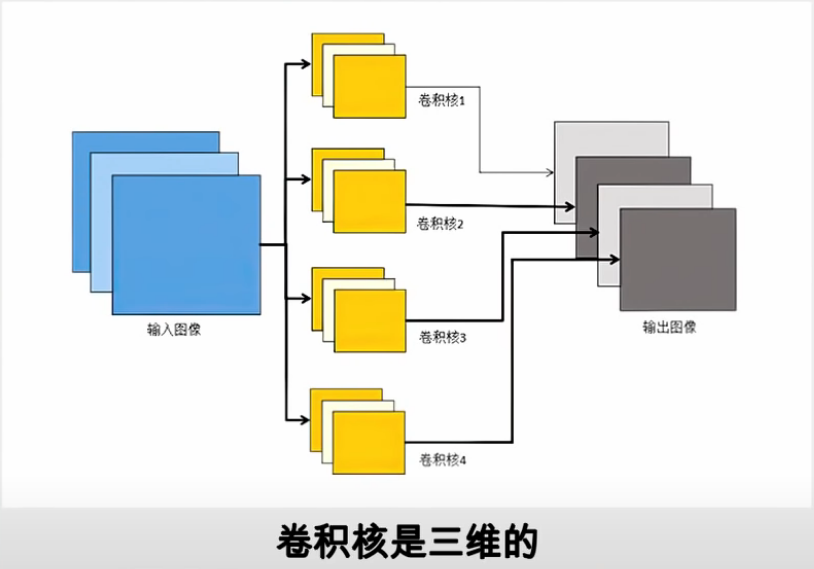
经过多次卷积,可以找到多种特征(线条、颜色等),输入到全连接网络进行训练